Navigation auf uzh.ch
Navigation auf uzh.ch
Operations with negation are performed over a positive relation p and a negative relation relation n, given a θ condition that determines the tuples that match. The result of a temporal-probabilistic operation with negation includes, at each time point, the probability with which a tuple of the positive relation p matches no tuple in the negative relation n under a predicate θ. Firstly, it includes output tuples that span subintervals when only tuples of the positive relation p are valid. In such cases, output intervals might be determined by starting or ending points of input tuples that are not valid during the output interval. Secondly, TP operations with negation produce outputs that indicate, at each time point, the probability of a tuple p1 in the positive relation not matching any valid tuple in the negative relation because all of them are false. In this case, an output interval T is determined based on the starting and ending points of p1 and of all the tuples of n that are valid over T and match p1 under θ.
In temporal-probabilistic (TP) databases, the combination of the temporal and the probabilistic dimension adds significant overhead to the computation of operations with negation, requiring for solutions that are more demanding than pairwise comparisons. In this work we propose algorithms for the efficient computation of the output intervals and lineage expressions on temporal-probabilistic operations with negation (set-difference, outer joins, anti join) that can be integrated in the kernel of PostgreSQL and we also propose means to get useful insights on their results.
Consider Migros, the leading supermarket branch in Switzerland that has multiple stores all over the country and that also offers the possibility to order groceries via its website. The supermarket records data related to purchases of clients, online shopping carts, and inventory, i.e. information that can be used to predict the behavior of its clients and to guarantee they will not leave a store or cancel an order unsatisfied due to unavailability of an item they intended to buy. In Figure 1, relation A contains the products that customers buy during a month at Migros’ stores in Zurich, relation B contains the products that customers order via the website and relation C contains the products that are in stock in each store. Abbreviations HB and OE refer to the stores in Hauptbahnhof (Central Station) and in Oerlikon, respectively. M-budget, Farmer, Alnatura and Milupa are four of the brands with products sold in Migros. More specifically, tuple a1 from relation A indicates that, at each day from the 1st until the 8th of the month, 'Ann shops cola in the physical store in HB' with probability 0.6. There is no other tuple in A that predicts the probability of 'Ann buying cola' over an interval overlapping with [01,08).
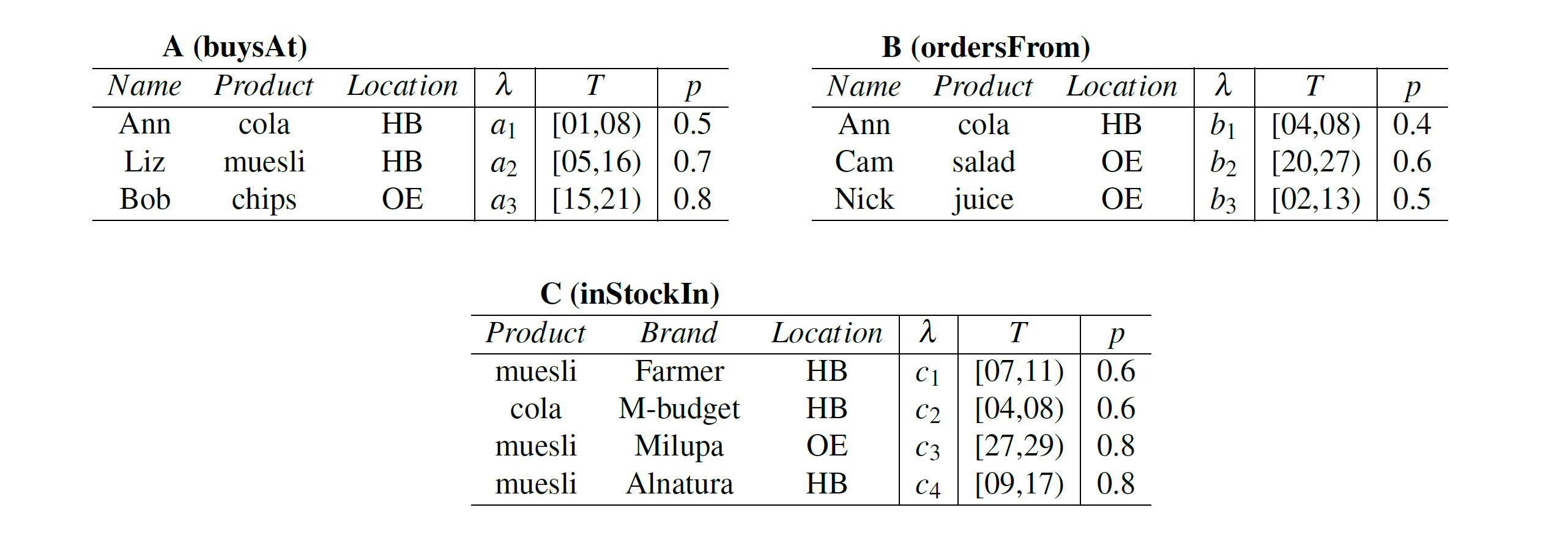
Assume the supermarket wants to determine, at each time point, the probability that a client intends to buy a product in a physical store and not online, and the product is in stock in this store. The algebra expression for this query is: Q = (A -Tp B) ⟕TpC, i.e., the set-difference of relations A and B, followed by a left outer-join with relation C. The result of the temporal-probabilistic set-difference includes the products that a client buys in a physical store but does not order from the website. The result of the temporal-probabilistic left outer-join computes at each time point, for all clients, the probability for each of their requested products to be in stock.
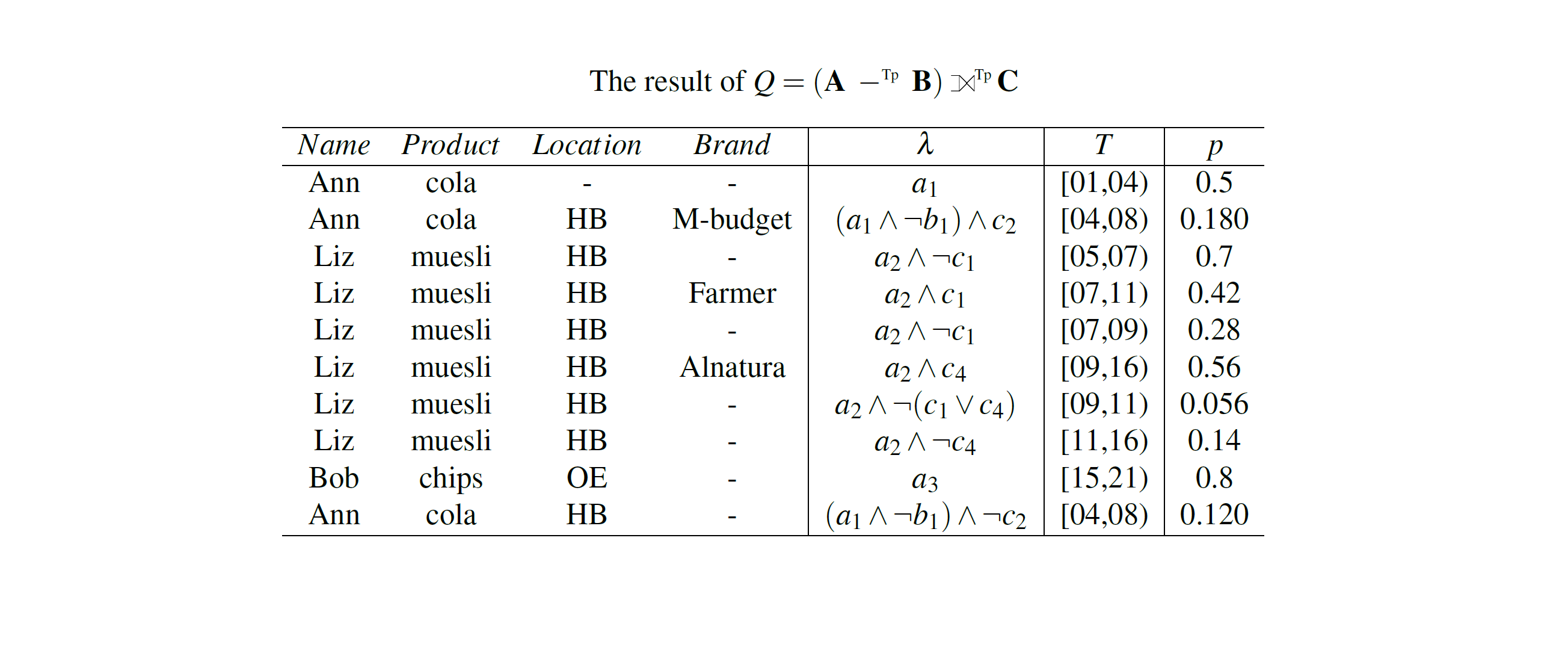
The output tuple 'Ann, cola, HB, M-budget', (a1 ∧ ¬ b1) ∧ c2, [04,08), 0.180) indicates that for each time point from the 4th until the 8th of the month, 'Ann buys cola from the brand M-budget in the store in HB and cola is in stock' with probability 0.180. At each time point in [04,08), for the fact '('Ann,cola, HB) to be true, the following must hold in a possible state of the database: (a) Ann intends to buy cola from M-budget in HB (a1), (b) Ann does not order cola online from the store in HB (¬b1), and (c) Cola from M-Budget is available in HB (c1). These conditions are reflected in the lineage expression of this fact that is (a1 ∧ ¬ b1) ∧ c2. Given the lineage expression, the probability can be computed by multiplying the input probabilities a1.p (0.5), 1-b1.p (0.6) and c1.p (0.6). The interval [04,08) is maximal, i.e., it cannot be shortened or enlarged. It cannot be shortened because if it did, we would exclude time points that have the same lineage expression as the time points included. Similarly, it cannot be enlarged because at time points outside [04;08), there is a change in the input tuples that contribute to the fact '(Ann, cola, HB, M-budget)' since tuple b1 is no longer valid. The output tuple ('Liz, muesli, HB, -', a1 ∧ ¬ c1, [07,09), 0.28) indicates that for each time point from the 7th until the 9th of the month, 'Liz wants to buy muesli in HB' and muesli from any brand is not in stock with probability 0.28.
This work makes the following three contributions:
A. It simplifies the computation of TP set operations by introducing lineage-aware temporal windows, a mechanism that binds the output intervals with the lineage expressions of the pair of valid tuples, thus allowing for the filtering and finalization of candidate output tuples at the time when they are produced
B. It introduces the generalized lineage-aware temporal windows for the computation of TP outer-joins and TP anti-join where multiple tuples of each input relation can be valid at a time point. The windows are grouped into three disjoint categories that can be computed incrementally, allowing for a major improvement in the runtime of TP joins with negation.
C. It introduces three types of charts for the analysis of the top-k temporal-probabilistic results of a query, providing the user with the most important information to systematically modify the time-varying probability of result tuples.
The source code (about 20MB gzipped tar archive) is available for download here. It contains compilation and installation instructions as well as sample relations and queries.
