18.02.2015New Working Paper "The Efficient Frontier in Randomized Social Choice"

Since the celebrated Gibbard-Satterthwaite impossibility results and Gibbard's 1977 extension for randomized rules, it is known that strategyproofness imposes severe restrictions on the design of social choice rules. In this paper, we employ approximate strategyproofness and the notion of score deficit to study the possible and necessary trade-offs between strategyproofness and efficiency in the randomized social choice domain.

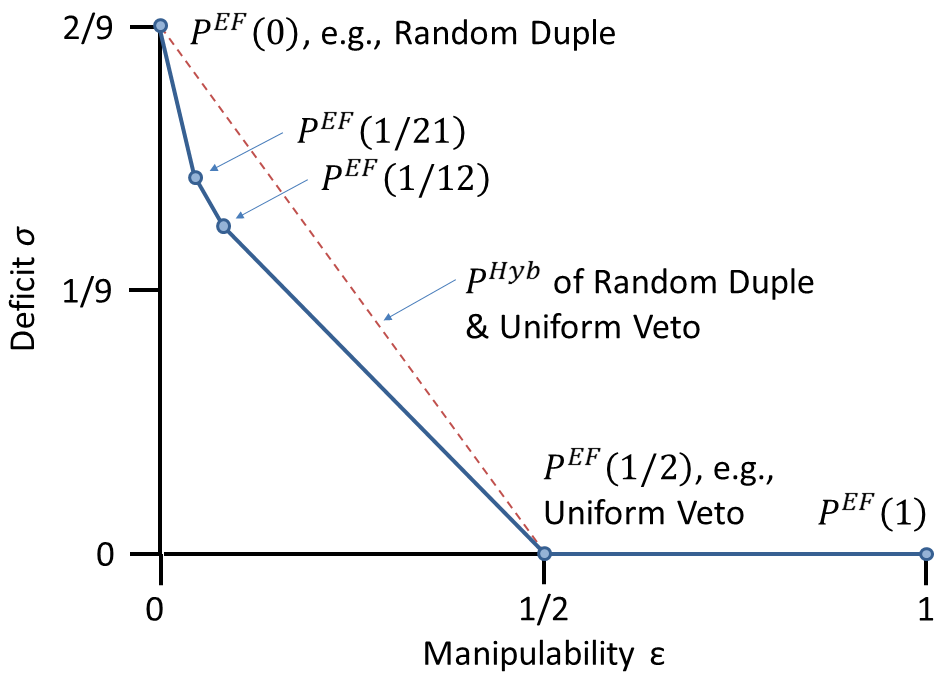
In particular, we analyze which social choice rules make optimal trade-offs, i.e., we analyze the efficient frontier. Our main result is that the efficient frontier consists of two building blocks: (1) we identify a finite set of manipulability bounds B and the rules that are optimal at each of them; (2) for all other bounds not in B, we show that the optimal rules at those bounds are mixtures of two rules that are optimal at the two nearest manipulability bounds from B. We provide algorithms that exploit this structure to identify the entire efficient frontier for any given scoring function. Finally, we provide applications of our results to illustrate the structure of the efficient frontier for the scoring functions v=(1,0,0) and v=(1,1,0). [pdf]